FM調頻 - moerjielovecookie

1 調制算法#

1.1 FM 信號描述#

用基帶調制信號去控制載波信號的瞬時頻率，使其按照調制信號的規律變化，當調制信號是模擬信號時，這個過程即為調頻。調頻信號的時域表達式如下：

S_{FM}(t)=A_m\times \cos[\omega_ct+K_f \int^{t}_{0}m(\tau)d\tau]\tag{1}

其中，$A_m$ 為載波振幅，$K_f$ 為調頻靈敏度（單位為 $rad/(s\cdot V)$），$m (t)$ 是調制信號，$cos\omega_c t$ 為載波，$\omega_c$ 為載波角頻率。
根據 (1) 式，可算出 FM 信號相對於載波頻率的瞬時頻偏為：

\frac{d\left[K_f\int_0^tm(\tau)d\tau\right]}{dt}=K_fm(t)\tag{2}

由（1）式可知，FM 信號相對於載波相位的瞬時相位偏移隨 $m (t)$ 的積分呈線性變化，由（2）式可知，FM 信號相對於載頻的瞬時頻率頻移隨 $m (t)$ 呈線性變化，比例系數都為 $K_f$。用 $k_f$ 表示調頻靈敏度（單位 Hz/V），關係為 $K_f=2\pi k_f$。
FM 的調頻指數 $\beta$ 為：

\beta=\frac{k_f |m(t)|_{max}}{W}\tag{3}

其中 $W$ 是基帶信號 $m (t)$ 的帶寬或最高頻率。

1.1.1 窄帶調頻（NBFM）#

將由 $m (t)$ 引起的最大瞬時相位偏移遠小於 30° 的情況稱為窄帶調頻。窄帶調頻的帶寬較窄，傳輸數據量有限，主要應用於無線語言的傳輸。

|K_f\int_0^tm(\tau)d\tau|\ll\frac\pi6 \tag{4}

此時，式（1）可以近似為：

\begin{aligned}s_{NBFM}(t)&=Acos\left[\omega_ct+K_f\int_0^tm(\tau)d\tau\right]\\\\&=Acos(\omega_ct)cos{\left[K_f\int_0^tm(\tau)d\tau\right]}-Asin(\omega_ct)sin{\left[K_f\int_0^tm(\tau)d\tau\right]}\\\\&\approx Acos(\omega_ct)\cdot1-Asin(\omega_ct)\cdot K_f\int_0^tm(\tau)d\tau\\\\&=Acos(\omega_ct)-\left[AK_f\int_0^tm(\tau)d\tau\right]sin(\omega_ct)\end{aligned}\tag{5}

對其做 FFT 變換，得到窄帶調頻信號的頻譜為：

S_{NBFM}(\omega)=\pi A\left[\delta(\omega+\omega_c)+\delta(\omega-\omega_c)\right]+\frac{AK_f}{2}\left[\frac{M(\omega-\omega_c)}{\omega-\omega_c}-\frac{M(\omega+\omega_c)}{\omega+\omega_c}\right]\tag{6}

其中 $M (\omega)$ 是調制信號 $m (t)$ 的頻譜。與 AM 信號不同的是，NBFM 信號的兩個邊帶分別乘了因式 $1/(\omega-\omega_c)\text { 和 } 1/(\omega+\omega_c)$，由於因式是與頻率有關的函數，所以其加權是頻率加權，加權的結果引起了調制信號頻譜失真，而且 NBFM 的一個邊帶與 AM 反相。

1.1.2 寬帶調頻（WBFM）#

當不滿足式（4）的條件時，稱為寬帶調頻。寬帶調頻佔用的頻帶較寬，傳輸數據量大，主要用於調頻立體聲廣播。WBFM 的時域表達式無法簡化，當 $m (t)=A_m \cos (\omega_m t)$ 時，帶入式（1）可得：

\begin{aligned}s_{WBFM}(t)&=Acos\left[\omega_ct+K_f\int_0^tA_mcos(\omega_m\tau)d\tau\right]\\\\& =Acos\left[\omega_ct+\frac{K_fA_m}{\omega_m}sin(\omega_mt)\right]\\\\& =Acos[\omega_ct+\beta sin(\omega_mt)]\\\\& =A\sum_{n=-\infty}^\infty J_n(\beta)cos[(\omega_c+n\omega_m)t]\end{aligned}\tag{7}

式中 $J_n (\beta)$ 為第一類 n 階貝塞爾函數，是調頻指數 $\beta$ 的函數。
頻譜為：

S_{WBFM}(\omega)=\pi A\sum_{n=-\infty}^\infty J_n(\beta)\left[\delta(\omega-\omega_c-n\omega_m)+\delta(\omega+\omega_c+n\omega_m)\right]\tag{8}

1.2 FM 信號的帶寬#

寬帶調頻信號的頻譜包含無窮多個頻率分量，因此理論上調頻信號的頻帶寬度為無限寬。但是，實際上邊頻幅度 $J_n (\beta)$ 隨著 n 的增大而減小，因此取適當的 n 值使邊頻分量小到可以忽略的程度即可近似認為 FM 信號具有有限帶寬。通常原則為信號的頻帶寬度應包括幅度大於未調載波的 10% 以上的邊頻分量。根據經驗，當 $\beta \geq 1$ 時，選取邊頻數 $n=\beta +1$ 即可，因為大於 $\beta+1$ 的邊頻幅度均小於 0.1。
根據這個經驗，FM 信號的有效帶寬為：

BW_{FM}=2(\beta+1)W\tag{9}

這個公式即為卡森公式。

2 FM 調制方法#

2.1 直接調頻法#

直接調頻法是用調制信號 $m (t)$ 直接控制高頻振盪器，讓回路元件的參數發生改變，使其輸出頻率按調制信號的規律線性地變化，常用的元件是變容二極管。直接調頻法的主要優點是在實現線性調頻的要求下，可以獲得較大的頻偏，且實現電路簡單；主要缺點是頻率穩定度不高，往往需要採用自動頻率控制系統來穩定中心頻率。

2.2 間接調頻法#

間接調頻法又被稱為倍頻法。先將調制信號積分，然後對載波進行調相，產生一個 NBFM 信號，再經過 $n$ 次倍頻器得到 WBFM 信號。優點是頻率穩定性高，缺點是需要多次倍頻和混頻，電路複雜。

2.3 正交調制法#

將式（1）進行三角展開，可得：

\begin{aligned}s_{FM}(t)&=Acos\left[\omega_ct+K_f\int_0^tm(\tau)d\tau\right]\\\\&=Acos(\omega_ct)cos\left[K_f\int_0^tm(\tau)d\tau\right]-Asin(\omega_ct)sin{\left[K_f\int_0^tm(\tau)d\tau\right]}\end{aligned}\tag{10}

流程如下：

對調制信號 $m (t)$ 進行積分，得到 $\Phi=K_f\int^{t}_{0} m (\tau) d\tau$
對積分後的信號分別取餘弦和正弦，得到 I 路數據 $I (t)=\cos (\Phi)$ 與 Q 路數據 $Q (t)=\sin (\Phi)$
分別乘上載波 $A\cos (\omega_c t)$ 與 $-A\sin (\omega_ct)$ 後相加，即可得到 FM 信號 $s_{FM}(t)=I (t) Acos (\omega_ct)-Q (t) Asin (\omega_ct)$

3 FM 信號格式#

我國的 FM 系統的調制頻偏為 150kHz，分布在 87MHz~107.9MHz 頻段。
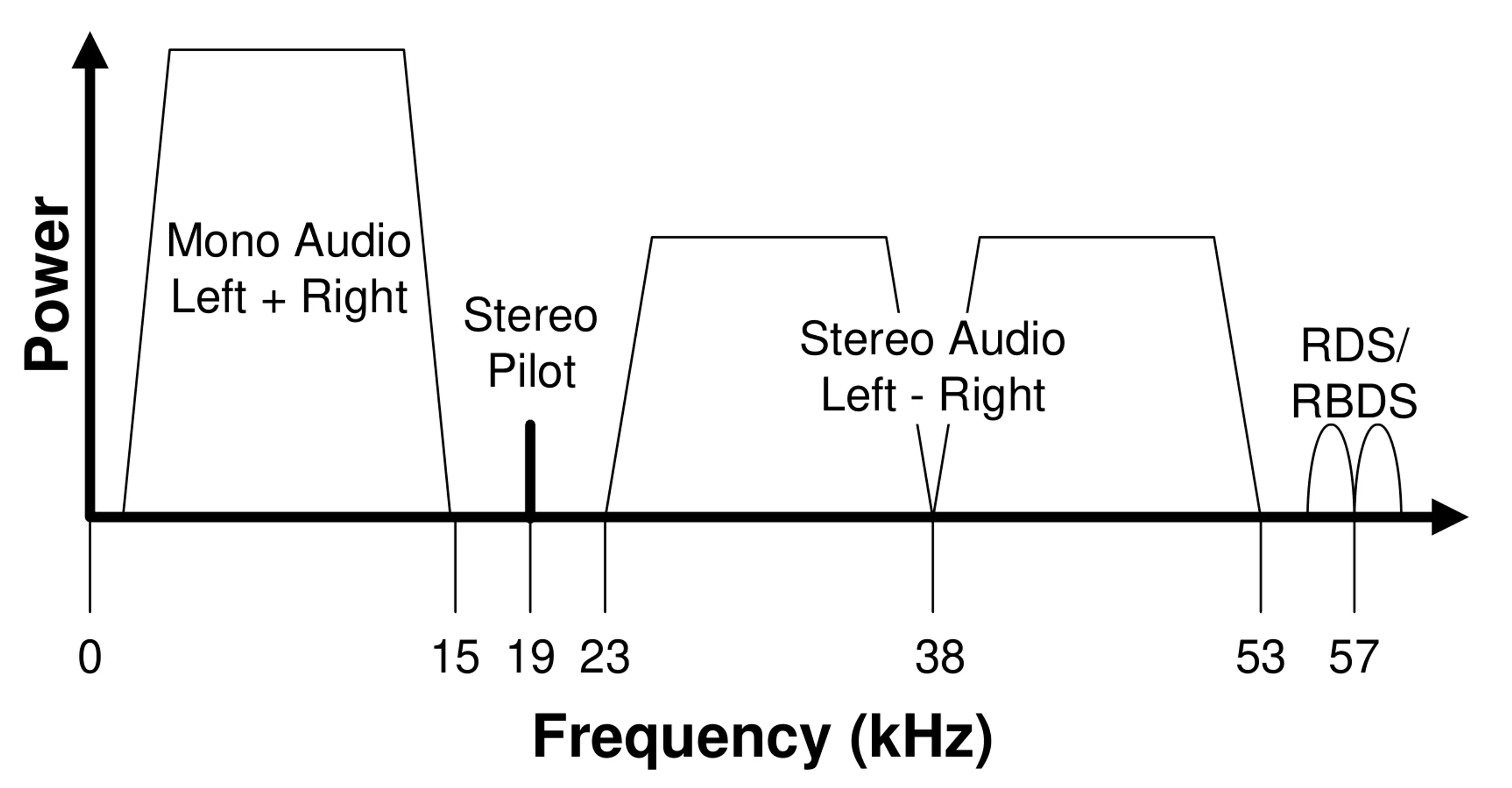
其中基帶信號為 MPX 信號，包含了單聲道（0~15kHz），導頻（19kHz），立體聲副載波（中心頻率 38kHz），RDS 數據（中心頻率 58kHz）。其頻譜成分如下：
MPX 信號的頻譜成分