Sawen_Blog

無線信道の典型的な特徴はフェージング現象です：信号の振幅が時間と周波数において変動します。加法ノイズは信号劣化の最も一般的な原因であり、フェージングはもう一つの原因で、無線信道において非加法的な信号の乱れを引き起こします。フェージングは多重経路伝播や障害物の遮蔽によっても引き起こされます。
フェージングは大きく分けて二種類に分類されます：大規模フェージングと小規模フェージング。移動機器が長距離移動する際（セルサイズの距離）に大規模フェージングが発生します。これは信号の経路損失（距離に関する関数）と大型障害物によって形成される影の影響によって引き起こされます。小規模フェージングは、移動機器が短距離内で移動する際に、多くの経路の干渉によって信号レベルが急速に変動することによって引き起こされます。

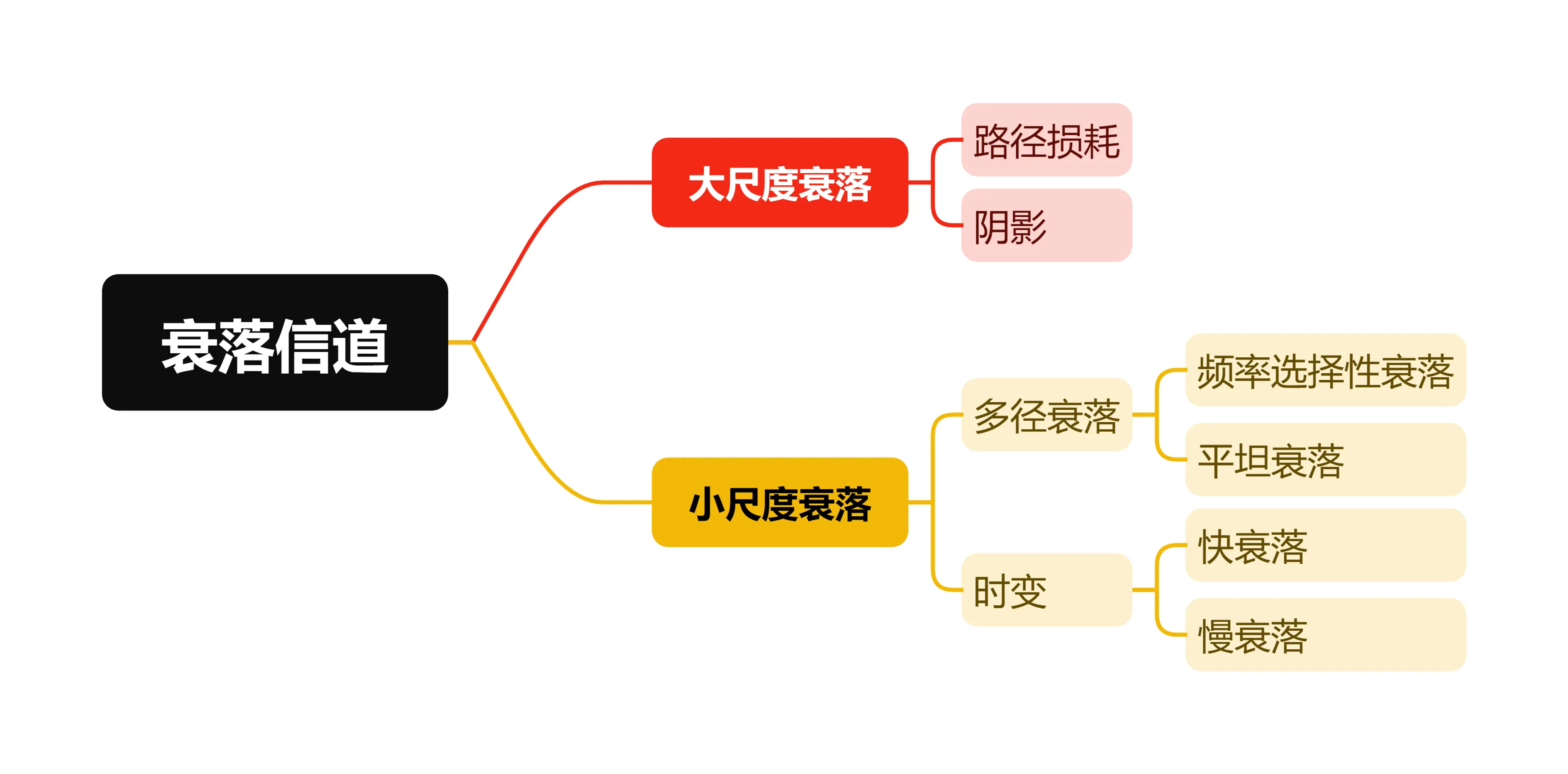
1 大規模フェージング#

1.1 一般的な経路損失モデル#

自由空間伝播モデルは、視距環境における信号受信強度を予測するために使用されます。衛星通信システムで一般的に使用されます。

ここで：
$P_t$ は送信出力、単位：W
$d$ は送信機と受信機の距離、単位：m
各向異性アンテナの場合、送信アンテナゲインは $G_t$、受信アンテナゲインは $G_r$
$L$ は伝播環境に依存しないシステム損失を示し、実際のハードウェアシステムにおける全体的な減衰を表します
システムハードウェアに損失がないと仮定すると、自由空間経路損失は次のようになります：

距離とアンテナゲインの違いに応じて、自由空間経路損失は図のようになります：

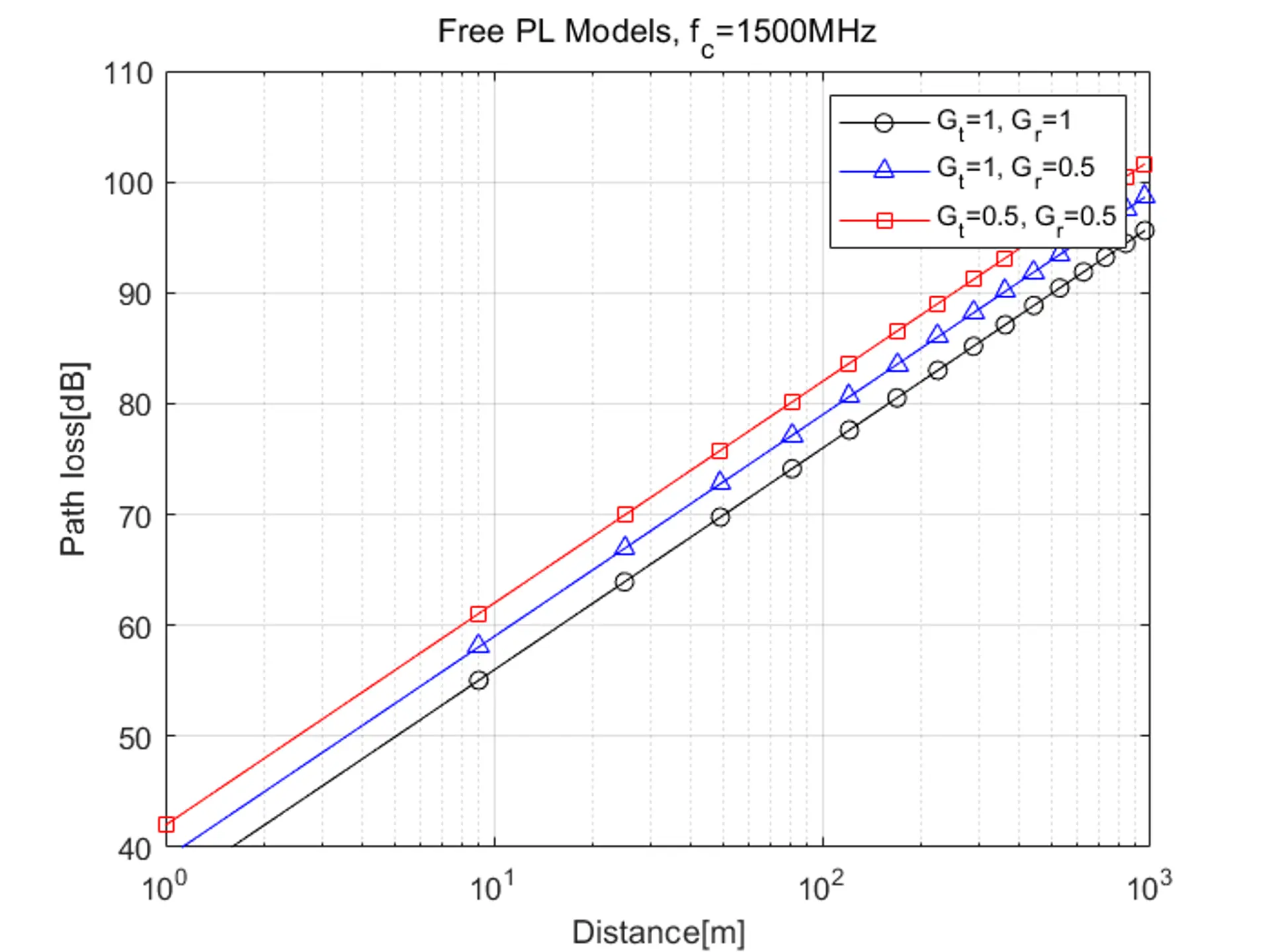
アンテナゲインがない場合、式は次のように簡略化できます：

対数距離経路損失モデルは次のようになります：

ここで、$d_0$ は参照距離であり、異なる伝播環境で異なります。例えば、大範囲をカバーするセルシステム（半径が 10km を超える）では、通常 $d_0$ を $1km$ と設定します；セル半径が $1km$ または非常に小さい半径のマイクロセルシステムでは、それぞれ $100m$ または $1m$ に設定できます。
経路損失指数 $n$ は伝播環境によって決まります。

環境	経路損失指数（n）
自由空間	2
都市セル	2.7~3.5
都市セルの影	3-5
建物内の視距伝送	1.6-1.8
建物内の障害物群	4-6
工場内の障害物遮蔽	2-3
対数距離経路損失モデルの図は次のようになります：
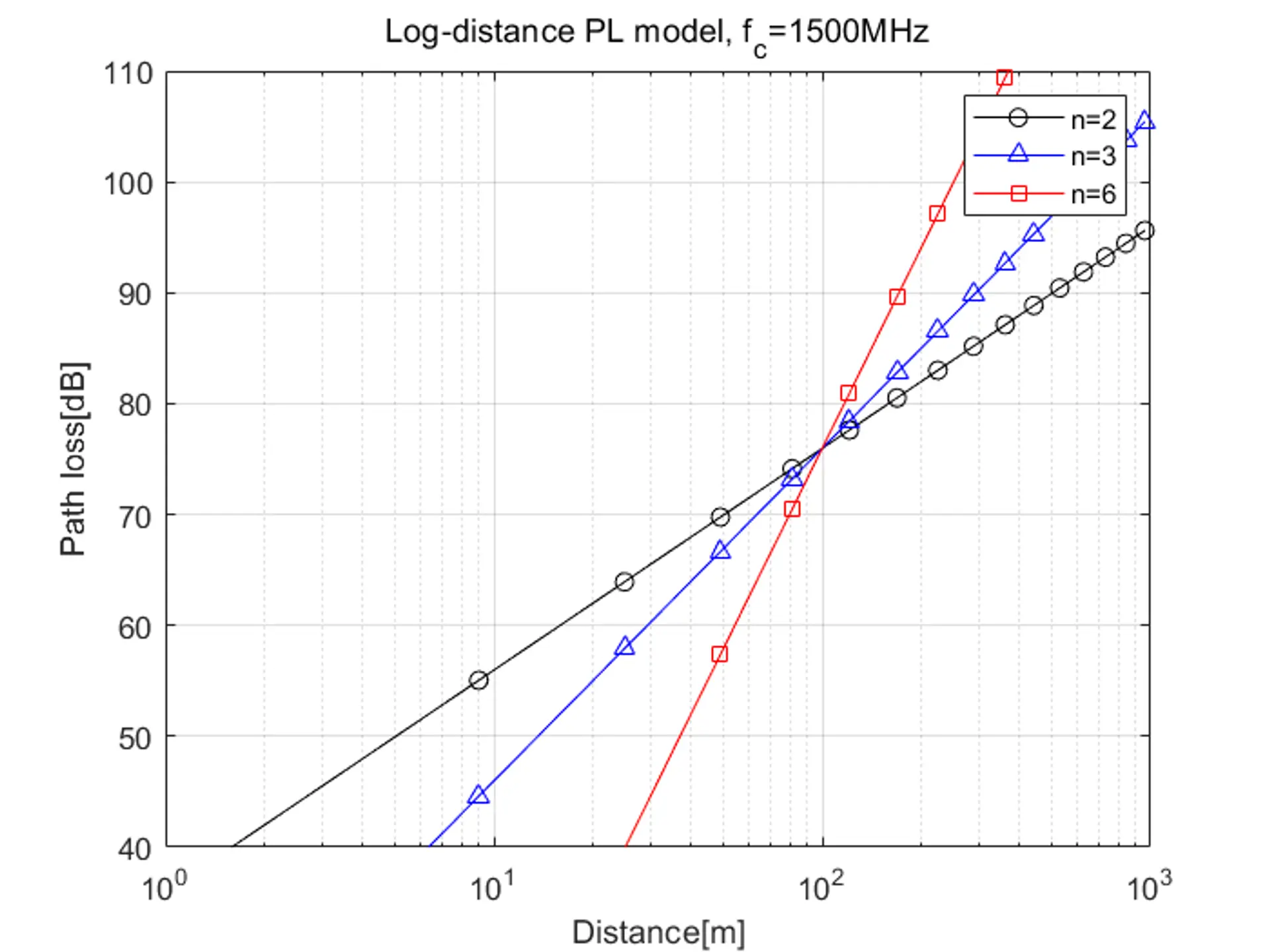周囲の環境は受信機の実際の位置によって変化するため、送信機と受信機の間の距離が同じであっても、各経路には異なる経路損失があります。より現実的な環境を設計する際には、対数正規影のモデルがより実用的です。$X_{\sigma}$ を平均が $0$、標準偏差が $\sigma$ のガウス乱数変数とすると、対数正規影フェージングモデルは次のようになります：

この時の示意図は次のようになります：

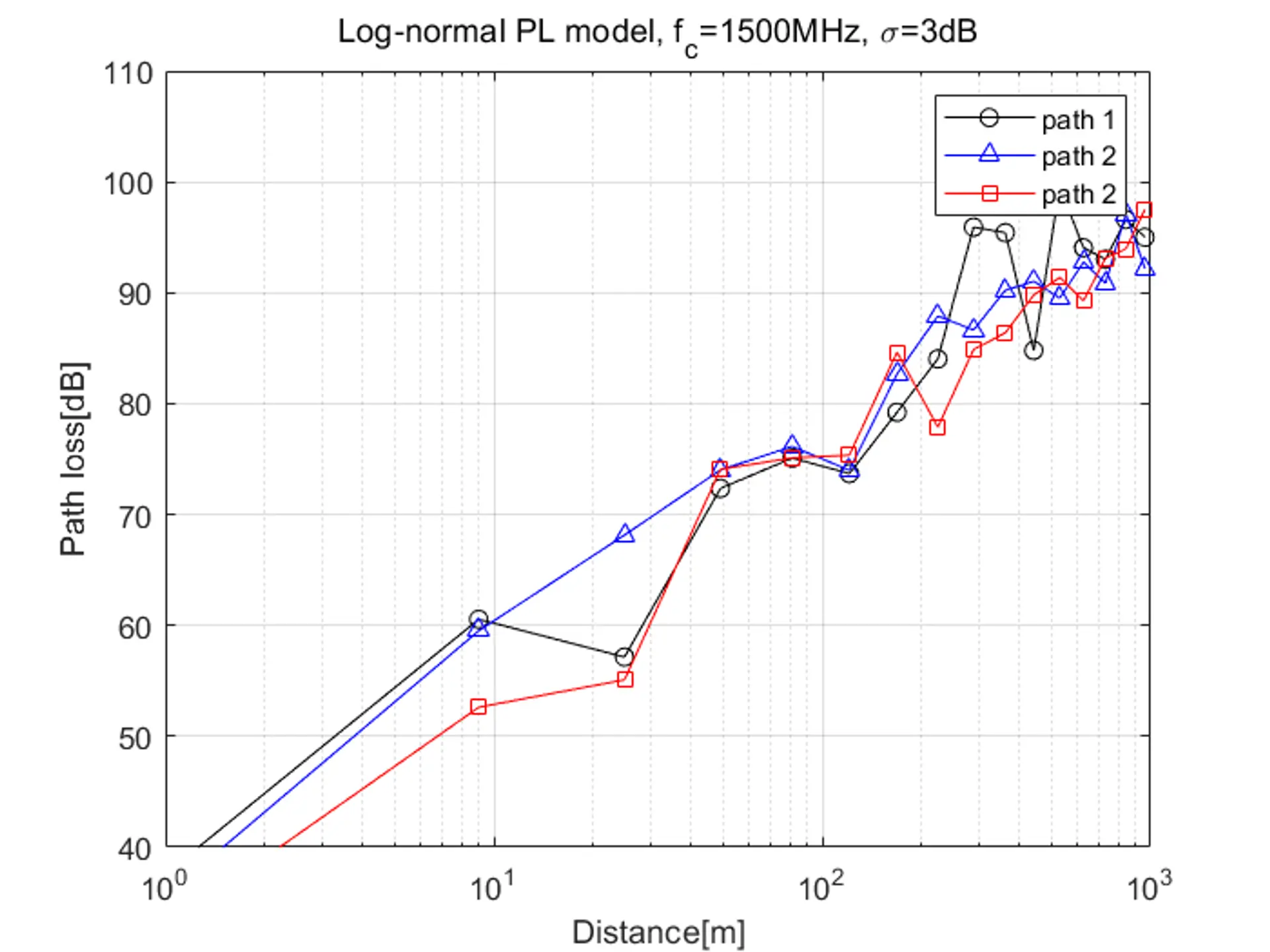
1.2 Okumura/Hata モデル#

都市地域の経路損失を予測するすべてのモデルの中で、Okumura モデルは最も多く採用されており、主にキャリア範囲が 500-1500MHz、セル半径が 1-100km、アンテナ高さが 30-1000m の移動通信システムに適しています。Okumura モデルにおける経路損失は次のように表されます：

ここで、$A_{\mathrm {MU}}\left (f,d\right)$ は周波数 $f$ における中程度の起伏減衰因子、$G_{AREA}$ は特定地域の伝播環境ゲインです。
HATA モデルは Okumura モデルをさまざまな伝播環境に拡張し、都市、郊外、開けた土地を含み、現在最も一般的に使用される経路損失モデルです。送信アンテナの高さを $h_{Tx}[m]$、キャリア周波数を $f_c [MHz]$、距離を $d [m]$ とした場合、都市部における Hata モデルの経路損失は次のようになります：

ここで、$C_{Rx}$ は受信アンテナに関連する係数で、カバレッジ範囲の大きさによって異なります。
中程度のカバレッジ範囲の場合、$C_{Rx}$ の値は次のようになります：

ここで $h_{Rx}[m]$ は受信アンテナの高さです。
大きなカバレッジ範囲の場合、$C_{Rx}$ はキャリア周波数によって決まります：

郊外の場合、Hata モデルは次のようになります：

開けた土地の場合、モデルは次のようになります：