Sawen_Blog

無線信道的一個典型特徵是衰落現象：信號幅度在時間和頻率上的波動。加性噪聲是信號惡化的最普遍來源，衰落是另一種來源，其在無線信道中引起的是非加性的信號擾動。衰落也可由多徑傳播或障礙物遮蔽引起。
衰落大致分為兩種：大尺度衰落和小尺度衰落。當移動設備長距離移動時（小區大小距離）會產生大尺度衰落。它由信號的路徑損耗（關於距離的 func）和大型障礙物形成的陰影所引起的。小尺度衰落是當移動設備在較短距離內移動時，由多條路徑的相消或相長干涉引起的信號電平快速波動。

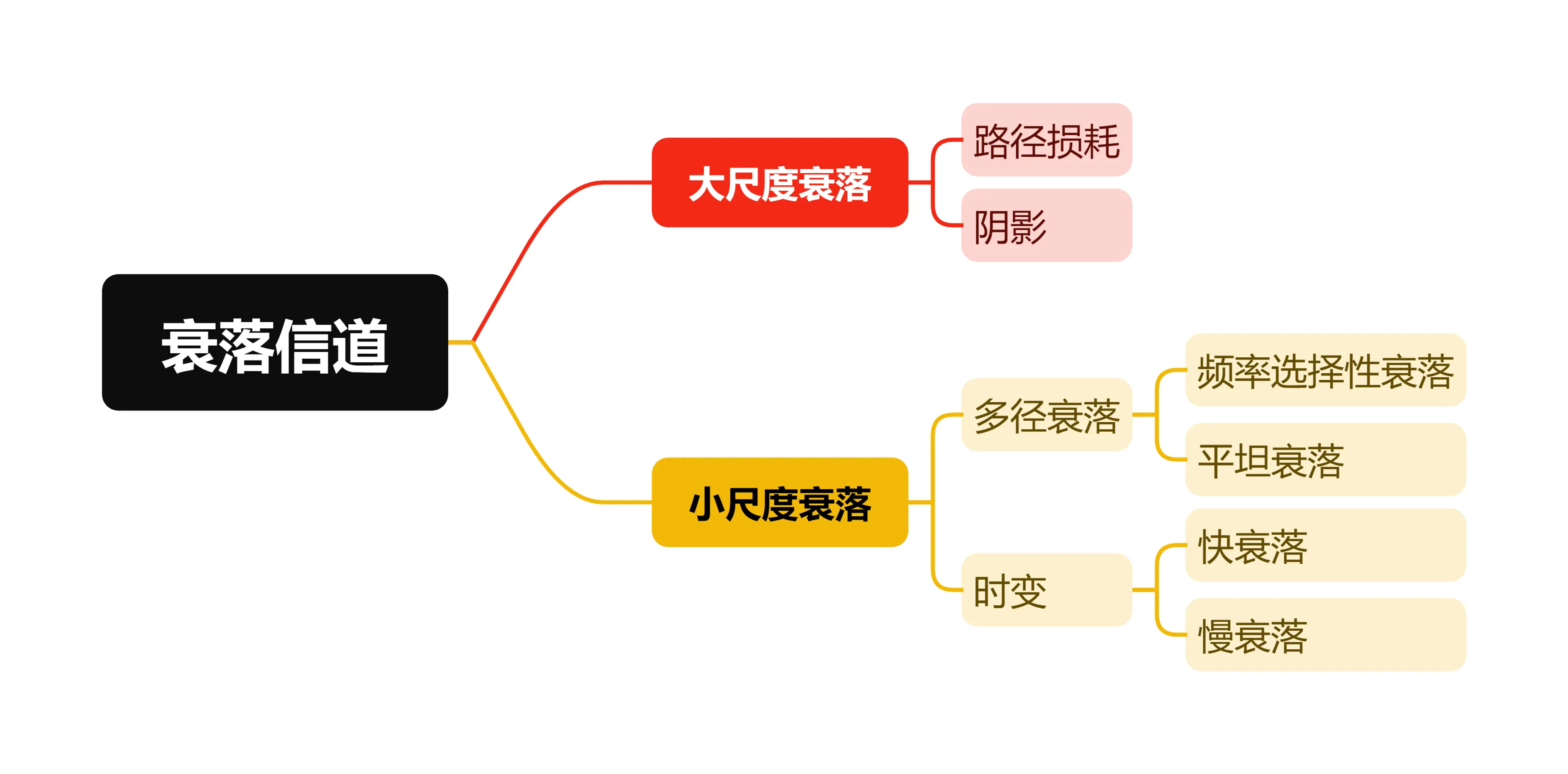
1 大尺度衰落#

1.1 一般路徑損耗模型#

自由空間傳播模型用於預測視距環境中信號接收的強度。常用於衛星通信系統。

其中：
$P_t$ 為發射功率，單位：W
$d$ 表示發射機與接收機的距離，單位：m
各向異性天線時，發射天線增益為 $G_t$，接收天線增益為 $G_t$
$L$ 為與傳播環境無關的系統損耗系統，表示實際硬體系統中的總體衰減
假設系統硬體沒有損耗，則自由空間路徑損耗為：

根據距離和天線增益不同，自由空間路徑損耗如圖所示：

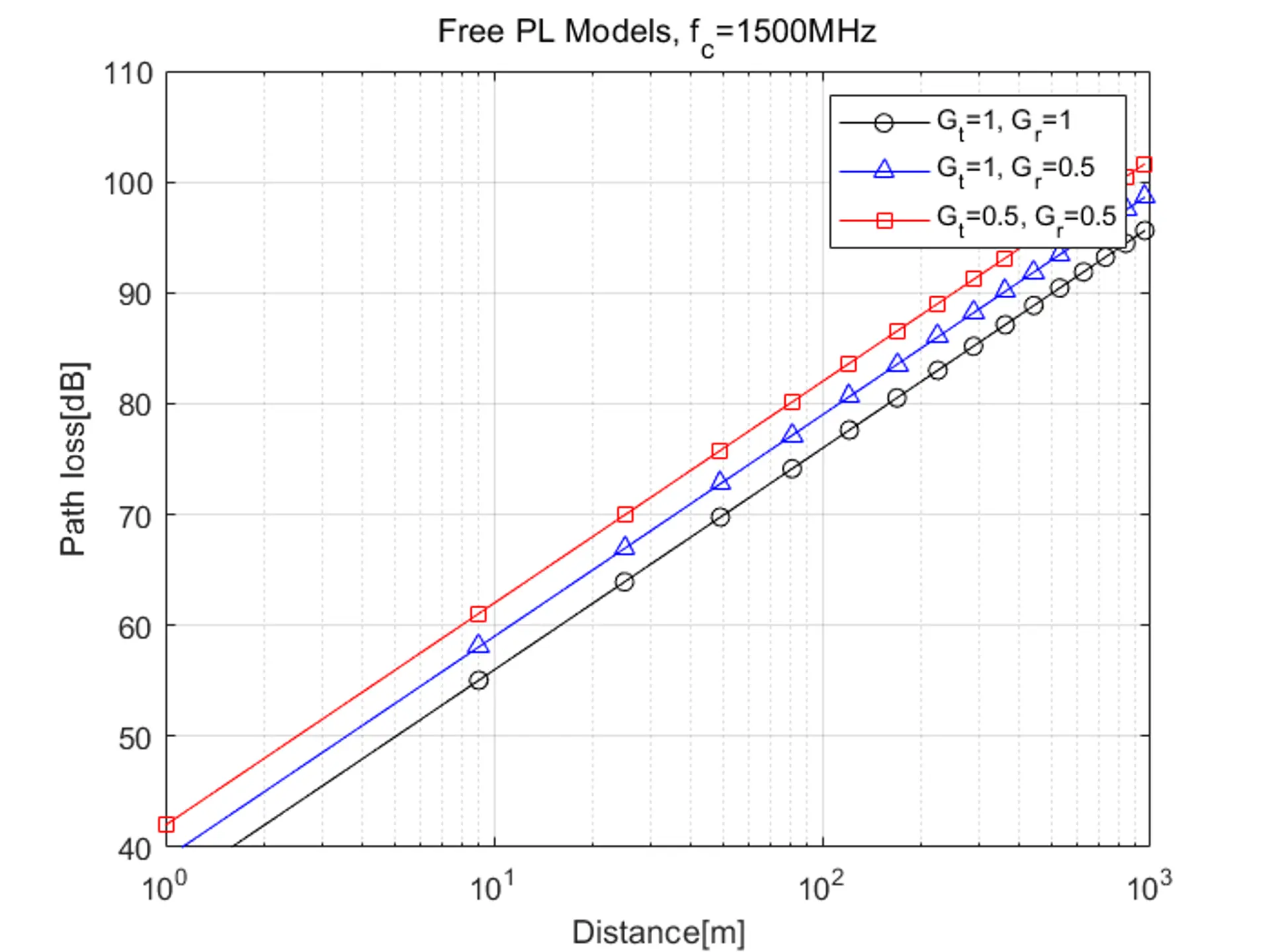
若沒有天線增益，則公式可以簡化為：

對數距離路徑損耗模型如下：

其中，$d_0$ 是一個參考距離，不同的傳播環境中參考距離不同。例如，大範圍覆蓋的蜂窩系統（半徑大於 10km），通常設置 $d_0$ 為 $1km$；對於小區半徑為 $1km$ 或具有極小半徑的微蜂窩系統，可以分別設置為 $100m$ 或 $1m$。
路徑損耗指數 $n$ 由傳播環境決定。

環境	路徑損耗指數（n）
自由空間	2
市區蜂窩	2.7~3.5
市區蜂窩陰影	3-5
建築物內視距傳輸	1.6-1.8
建築物內障礙物組隊	4-6
工廠內障礙物阻擋	2-3
對數距離路徑損耗模型圖如下：
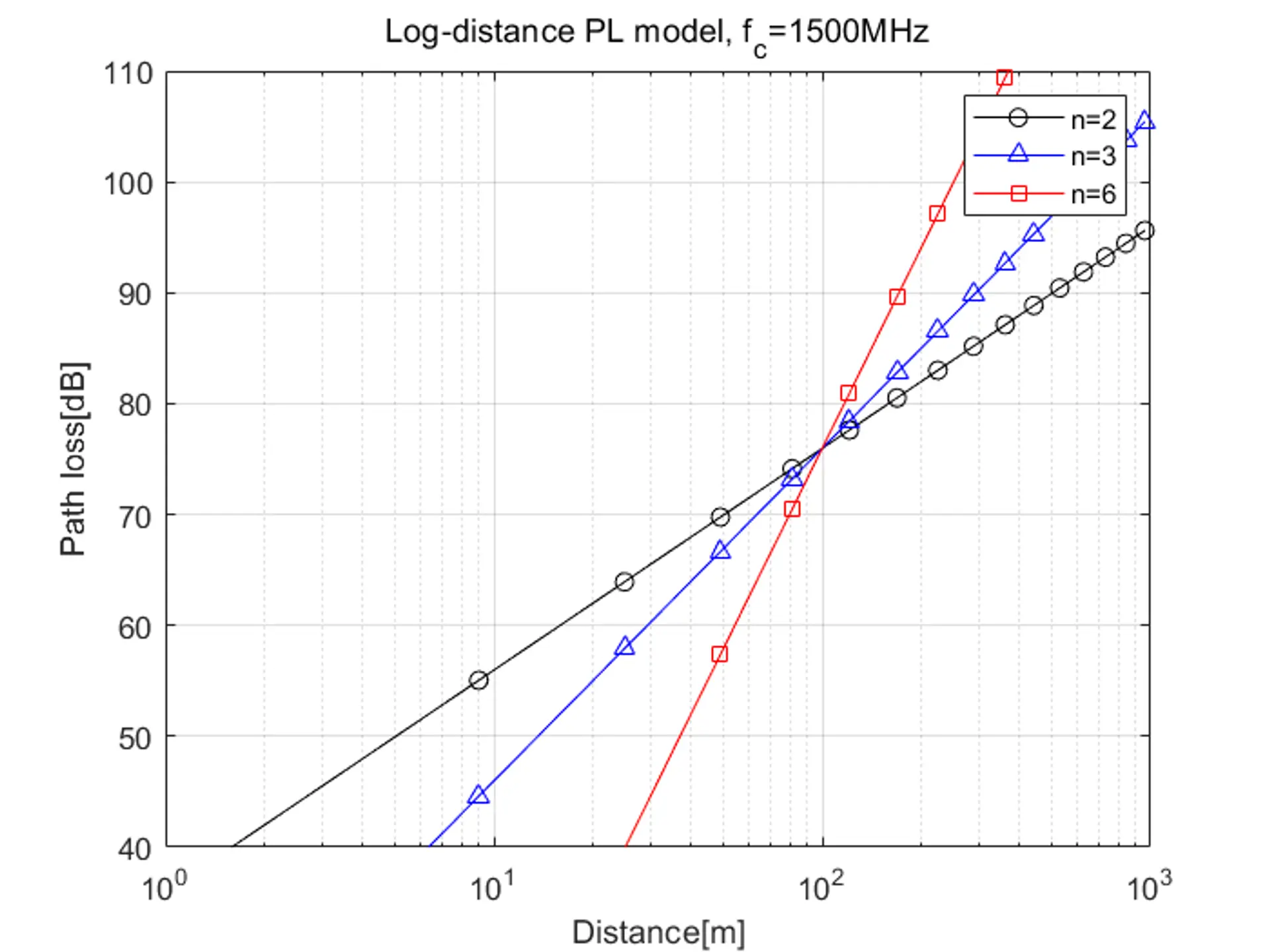由於周圍環境會隨著接收機的實際位置不同而改變，即使發射機到接收機之間的距離相同，每條路徑也有不同的路徑損耗。在設計更真實的環境時，對數正態陰影模型更加實用。令 $X_{\sigma}$ 表示均值為 $0$，標準差為 $\sigma$ 的高斯隨機變量，對數正態陰影衰落模型為：

此時示意圖為：

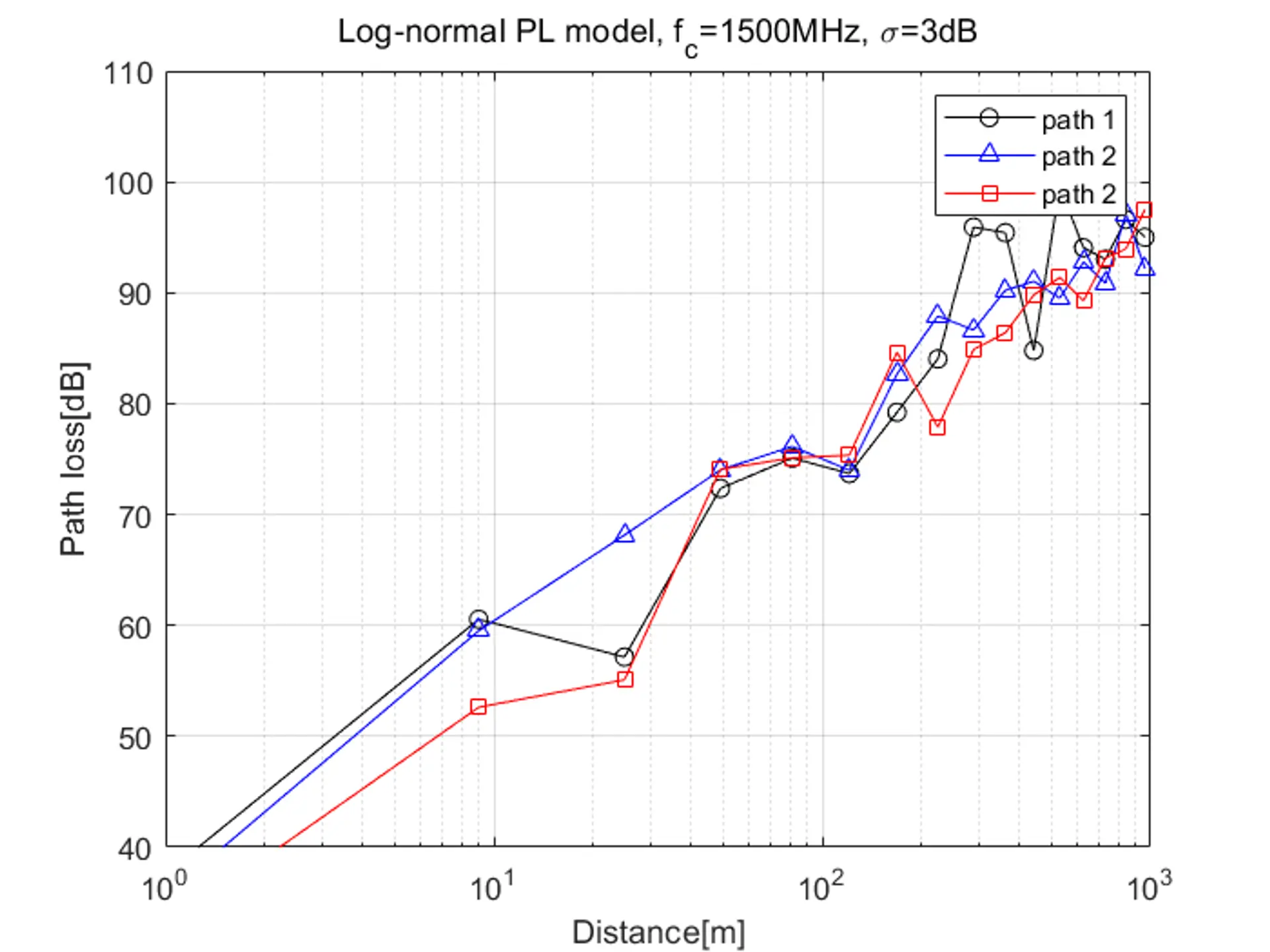
1.2 Okumura/Hata 模型#

在預測城市地區路徑損耗的所有模型中，Okumura 模型是被採用最多的一種，主要適用於載波範圍在 500-1500MHz，小區半徑為 1-100km，天線高度為 30-1000m 的移動通信系統。Okumura 模型中路徑損耗可以表示為：

其中，$A_{\mathrm {MU}}\left (f,d\right)$ 為頻率為 $f$ 處的中等起伏衰減因子，$G_{AREA}$ 為具體地區的傳播環境增益。
HATA 模型將 Okumura 模型擴展到了各種傳播環境，包括城市、郊區、開闊地，為當今最常用的路徑損耗模型。對於發射天線高度為 $h_{Tx}[m]$, 載波頻率為 $f_c [MHz]$，距離為 $d [m]$，在市區中 Hata 模型的路徑損耗為：

其中，$C_{Rx}$ 為與接收天線相關的係數，取決於覆蓋範圍的大小。
對於中等大小的覆蓋範圍，$C_{Rx}$ 取值為：

其中 $h_{Rx}[m]$ 為接收天線的高度。
對於大的覆蓋範圍，$C_{Rx}$ 取決於載波頻率：

對於郊區，Hata 模型為：

對於開闊地，模型為：